I thought that it could be good excercise to write script that will use graphs to find "cheapest way" using some algorithm. I know that there are probably plenty of ready, well tested libraries which we can use but that's not the way - we don't want to use it, we want to create it!
Data
The most important thing is the data. I believe that we don't need a big dataset, I think that more crucial is that data should be easy to understand. I prepared some simple graph for that:
graph = {}
graph['London'] = {}
graph['London']['Paris'] = 466
graph['London']['Hanover'] = 817
graph['London']['Zurich'] = 942
graph['Hanover'] = {}
graph['Hanover']['Paris'] = 786
graph['Hanover']['Frankfurt'] = 350
graph['Hanover']['Zurich'] = 723
graph['Hanover']['Berlin'] = 285
graph['Hanover']['Dresden'] = 366
graph['Frankfurt'] = {}
graph['Frankfurt']['Hanover'] = 350
graph['Frankfurt']['Berlin'] = 546
graph['Frankfurt']['Dresden'] = 462
graph['Frankfurt']['Prague'] = 510
graph['Frankfurt']['Zurich'] = 410
graph['Paris'] = {}
graph['Paris']['Zurich'] = 604
graph['Paris']['Hanover'] = 773
graph['Paris']['Frankfurt'] = 573
graph['Zurich'] = {}
graph['Zurich']['Frankfurt'] = 410
graph['Zurich']['Prague'] = 683
graph['Berlin'] = {}
graph['Berlin']['Dresden'] = 193
graph['Berlin']['Warsaw'] = 574
graph['Berlin']['Kopenhaga'] = 439
graph['Kopenhaga'] = {}
graph['Dresden'] = {}
graph['Dresden']['Berlin'] = 193
graph['Dresden']['Prague'] = 149
graph['Dresden']['Warsaw'] = 621
graph['Prague'] = {}
graph['Prague']['Dresden'] = 149
graph['Prague']['Warsaw'] = 682
graph['Warsaw'] = {}
How to understand this graph? It's easy - each city has some connections at certain distances, for example graph['Zurich']['Prague'] = 683 means that from Zurich to Prague we have 683 kilometers. To make it more clear, I created visual version of this graph using graphviz.
require 'ruby-graphviz'
g = GraphViz.new( :G, :type => :digraph )
graph.keys.each { |city| instance_variable_set("@#{city.downcase}", g.add_nodes(city)) }
graph.each do |city, neighbors|
neighbors.each { |neighbor, _v| g.add_edges( eval("@#{city.downcase}"), eval("@#{neighbor.downcase}")) }
end
g.output( :png => "graph_preview.png" )
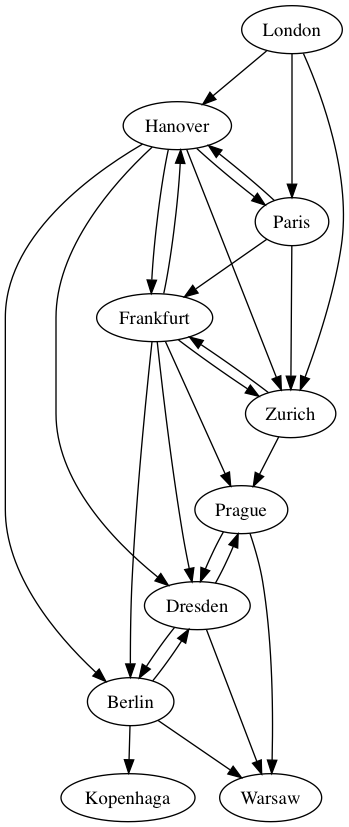
As you can see, we have several cities in the middle of our route, each city has some connections to other ones.
Algorithm
I've chosen the Dijkstra algorithm because it is quite simple and fits well to this task. Dijkstra algorith can help to find the cheapest way, what in our case means - the shortest way. This algorith is universal - we can use it to look for the the shortest path, the cheapest path, the easiest path or whatever we want. One important thing is that we can't use negative values in graphs. In our case it's impossible to have negative value, so we don't care, but in some cases we should (for example, for some cash operations where we can give money to someone and someone can give us money).
If you aren't familiar with Dijkstra algorithm, I recommend reading or watching a tutorial about it. This one looks good:
Implementation
I created the Dijkstra class. Please look at the code below:
class Dijkstra
def initialize(graph, start_point, stop_point)
@graph = graph
@start_point = start_point
@stop_point = stop_point
end
def find_cheapest_way
node = lowest_cost_node
while node do
cost = costs[node]
neighbors = graph[node]
neighbors.keys.each do |neighbor|
new_cost = cost + neighbors[neighbor]
if costs[neighbor].nil? || costs[neighbor] > new_cost
costs[neighbor] = new_cost
parents[neighbor] = node
end
end
processed << node
node = lowest_cost_node
end
self
end
def print_results
puts "Total distange: #{costs[stop_point]}"
puts "Way: #{way.join(' -> ').upcase}"
end
private
attr_reader :graph, :start_point, :stop_point
def processed
@processed ||= []
end
def parents
@parents ||= {}.tap do |parents_hash|
graph[start_point].each do |neighbor, _distance|
parents_hash[neighbor] = start_point
end
end
end
def costs
@costs ||= {}.tap do |costs_hash|
graph[start_point].each do |neighbor, distance|
costs_hash[neighbor] = distance
end
costs_hash[stop_point] = Float::INFINITY
end
end
def lowest_cost_node
lowest_cost = Float::INFINITY
lowest_cost_node = nil
costs.keys.each do |node|
new_cost = costs[node]
if new_cost < lowest_cost && !processed.include?(node)
lowest_cost = new_cost
lowest_cost_node = node
end
end
lowest_cost_node
end
def way
[].tap do |way|
way.unshift(stop_point)
parent = parents[stop_point]
while parent
way.unshift(parent)
parent = parents[parent]
end
end
end
end
How it works?
We can use our class quite simple:
cheapest_way = Dijkstra.new(graph, 'London', 'Warsaw').find_cheapest_way
cheapest_way.print_results
as result we should see:
Total distance: 1676
Way: LONDON -> HANOVER -> BERLIN -> WARSAW
Cool! But how does it work?
We initialized class with three attributes - our graph and name (key) of starting and ending point. Then we called #find_cheapest_way method that found our cheapest way. To print result we used #print_results that simple print distance and all waypoints.
Our trip starts from London, because of that we know four points: London's neighbors Paris, Hanover, Zurich and destination point Warsaw. We know distance to neighbors, but we don't know distance to destination point yet. In next steps algorith will be checking how it can move to other points in cheapest way.
At the end our costs will look like this:
{"Paris"=>466, "Hanover"=>817, "Zurich"=>942, "Warsaw"=>1676, "Frankfurt"=>1039, "Berlin"=>1102, "Dresden"=>1183, "Prague"=>1332, "Kopenhaga"=>1541}
We can understand them as - From start point to Paris we have 466km, to Hanover 817km, to Zurich 942km and so on.
And our parents:
{"Paris"=>"London", "Hanover"=>"London", "Zurich"=>"London", "Frankfurt"=>"Paris", "Berlin"=>"Hanover", "Dresden"=>"Hanover", "Prague"=>"Dresden", "Warsaw"=>"Berlin", "Kopenhaga"=>"Berlin"}
We have there informations about trip. Our destination was Warsaw, so we know that the previous city is Berlin and next one from Berlin is Hanover.
I hope it was quite interesting topic for you. If so, take a look for the Bellman-Ford algorithm where we can use even negative values.
